Annales BAC - Fonctions et dérivées
Exercice 1
Exercice tiré du sujet de septembre 2014 aux Antilles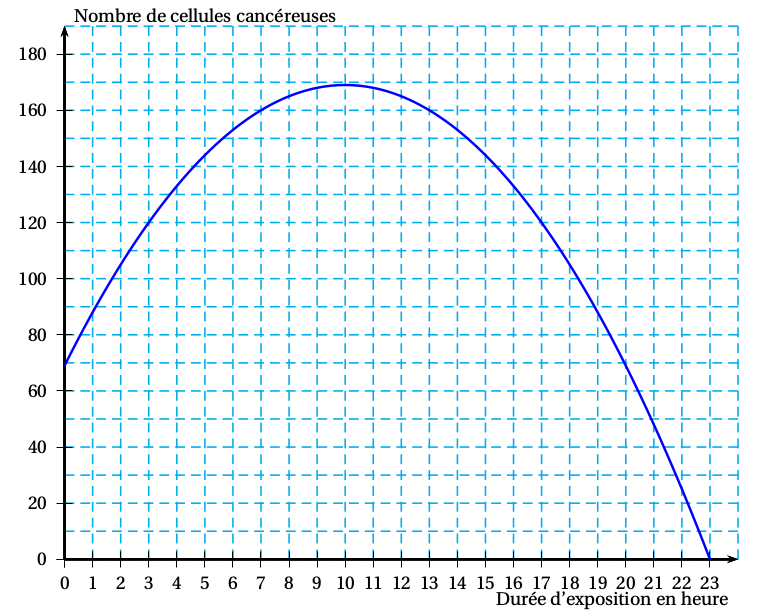 
Un laboratoire de recherches médicales observe « in vitro » la multiplication, par mitose accélérée, d’une cellule cancéreuse. Les chercheurs veulent étudier l’effet du rayonnement d’ondes millimétriques sur les cellules cancéreuses. Après une période de multiplication des cellules, on note t = 0, l’instant à partir duquel commence l’exposition au rayonnement d’ondes millimétriques. La courbe ci-dessous est la représentation graphique du nombre de cellules cancéreuses depuis le début du rayonnement.
AEtude graphique
1
Déterminer le nombre de cellules cancéreuses au début du rayonnement.
2
Déterminer la durée, approximative, d’exposition au rayonnement pour que le nombre de cellules cancéreuses redevienne celui qu’il était au début de l’exposition.
3
a
Après quelle durée d’exposition le nombre de cellules cancéreuses est-il maximum ?
b
Quelle est alors la valeur de ce maximum ?
4
Déterminer pendant quelle durée d’exposition le nombre de cellules cancéreuses est supérieur ou égal à 120.
5
Déterminer la durée d’exposition nécessaire pour détruire toutes les cellules cancéreuses.
BEtude théorique
Après observation, les chercheurs conviennent de modéliser l’évolution du nombre de cellules cancéreuses exposées à ce rayonnement par la fonction f définie sur l’intervalle \([0 ; 23]\) par $$ f (t) = -t^2 + 20 t + 69 $$ où \(t\) est la durée d’exposition et \(f (t)\) le nombre de cellules cancéreuses après t heures d’exposition à ce rayonnement.1
Calculer \(f (15)\) et interpréter le résultat par une phrase dans le contexte de l’exercice.
2
Calculer \(f' (t)\) pour \(t\) appartenant à l’intervalle \([0 ; 23]\), où \(f'\) est la fonction dérivée de la fonction \(f\) .
3
Étudier le signe de \(f' (t)\) sur l’intervalle \([0 ; 23]\).
4
Construire le tableau de variations de la fonction \(f\) sur l’intervalle \([0 ; 23]\).
5
En utilisant la question précédente, retrouver les résultats des questions 3.a. et 3.b. de la partie A.
Exercice 2
Exercice tiré du sujet de juin 2014 en métropole
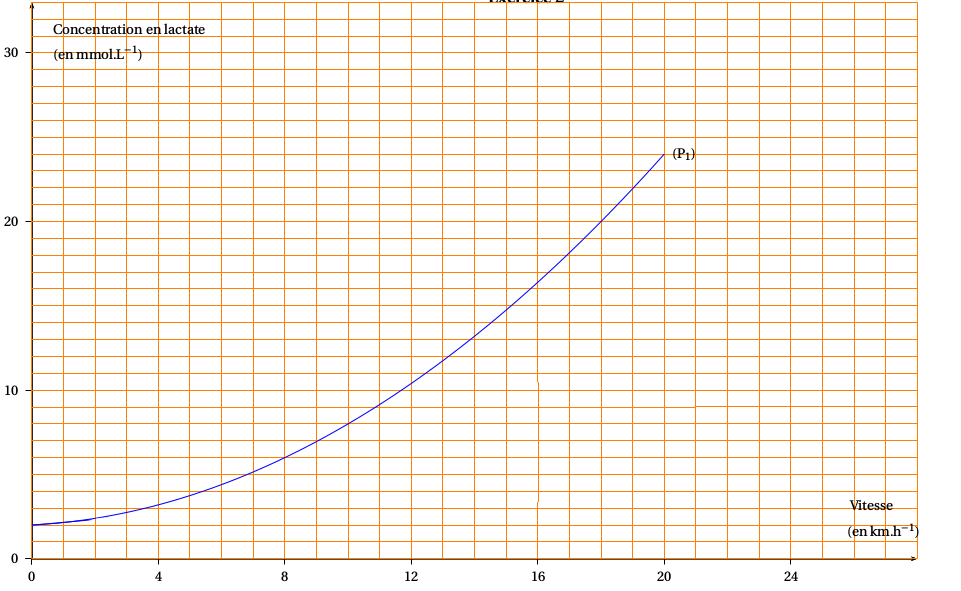On admet que cette courbe est la représentation graphique de la fonction g définie sur l’intervalle \([0 ; 20]\) par
$$ g (x) = 0,05 x^2 + 0,1x + 2
$$
On s’intéresse à la courbe représentant la lactatémie du coureur P 1.
On admet que cette courbe est la représentation graphique de la fonction g définie sur l’intervalle \([0 ; 20]\) par
$$ g (x) = 0,05 x^2 + 0,1x + 2
$$ 1
La fonction \(g'\) est la fonction dérivée de la fonction \(g\) . Déterminer \(g' (x)\) pour tout réel \(x\) appartenant à l’intervalle \([0 ; 20]\).
2
Déterminer \(g ' (8)\) et construire la tangente à la courbe représentant la fonction \(g\) au point d’abscisse \(8\). Justifier la construction.